
La matematica che ci fa capire di non sapere
I vetri di spin sono delle leghe formate da metalli nobili, nei quali viene sciolta una piccola quantità di ferro. Pur essendo materiali inesistenti in natura e dallo scarso interesse applicativo, sono tuttavia al centro dell'interesse dei fisici statistici da una cinquantina d'anni. Gli studi sui vetri di spin sono stati determinanti per l'assegnazione del Premio Nobel per la Fisica a Giorgio Parisi nel 2021.
L'interesse scientifico dei vetri di spin consiste nel fatto che costituiscono l'esempio paradigmatico di un sistema complesso, i cui elementi interagiscono tra loro in modo a volte cooperativo ed a volte avversario. La matematica sviluppata per comprenderne il comportamento può essere applicata a problemi che emergono in svariate discipline, dall'ecologia al machine learning e senza trascurare l'economia.
I vetri di spin sono dei sistemi magnetici, ovvero sistemi in cui i singoli elementi, gli spin, si comportano come piccoli magnetini. La loro peculiarità è la compresenza di legami di tipo ferromagnetico, che tendono ad allineare gli spin, con legami di tipo antiferromagnetico, che tendono ad orientarli in versi opposti. Questo fa sì che le configurazioni ad energia più bassa presentino della frustrazione residua: non è possibile trovare un arrangiamento degli spin che soddisfi tutti i legami. Le configurazioni frustrate inoltre sono raggruppate in un numero enorme (esponenziale!) di equilibri possibili. Tutto ciò è in stridente contrasto con quanto avviene nei sistemi puramente ferromagnetici, dove a bassa temperatura solo due stati sono ammissibili (spin allineati verso l'alto o spin allineati verso il basso).
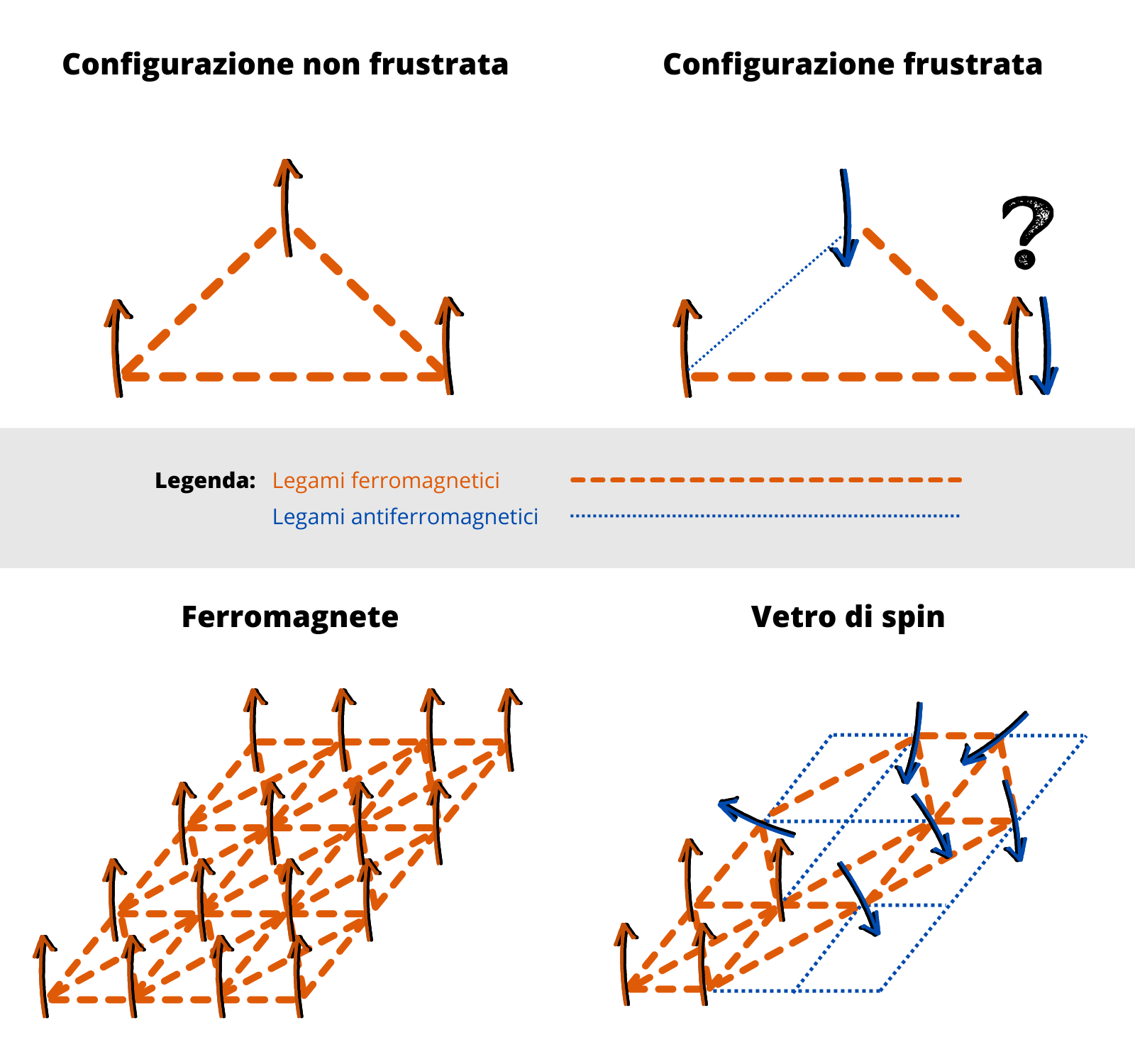
Illustrazione Weiwei Chen
Usando l'analogia con un ecosistema, il fatto di avere un alto numero di equilibri indica un ecosistema resiliente, capace di far fronte, per esempio, alla scomparsa di una specie, attraverso un numero limitato di riarrangiamenti. Un basso numero di equilibri descrive un sistema fragile, che necessita di numerosi e complicati riarrangiamenti per tornare in equilibrio e può, perciò, essere seriamente danneggiato, se non distrutto, da perturbazioni relativamente piccole.
Questa fenomenologia è stata ben chiarificata e descritta matematicamente nei sistemi che vivono in dimensione infinita, cosiddetti di campo medio, la cui soluzione è stata fornita da Parisi nel 1979 e poi meglio compresa negli anni successivi con l'aiuto di Marc Mézard (oggi professore ordinario alla Bocconi) e Michelangelo Virasoro.
"Uno dei temi più dibattuti," spiega Carlo Lucibello, assistant professor del Dipartimento di Computing Sciences e coautore, con Parisi e altri, di un articolo appena pubblicato da Physical Review Letters, "è fino a che punto la fenomenologia di campo medio si applichi in bassa dimensionalità."
Sappiamo infatti che in dimensione 1, ovvero su una catena di spin, il sistema è sempre in una fase paramagnetica, per cui abbassando la temperatura non ci sono transizioni né ad una fase di spin glass con i suoi numerosi equilibri né ad una semplice fase ferromagnetica.
"Esiste una cosiddetta dimensione superiore critica," dice ancora Lucibello, "al di sopra della quale vale la teoria di campo medio, che ci permette di predire gli esponenti che governano la transizione. Al momento però, nessuno sa dire con certezza quale sia questa dimensione (5, 6, o un numero non intero?) e che cosa succeda al di sotto."
Il paper appena pubblicato da Lucibello e coautori presenta una nuova tecnica matematica che permette di analizzare i sistemi a dimensionalità finita. La nuova teoria prevede una dimensione superiore critica di 8, per cui possiamo ragionevolmente concludere che gli spin glass del nostro mondo tridimensionale difficilmente saranno descritti da una teoria di campo medio e che c'è ancora tanto lavoro da fare in questo ramo della fisica teorica.

Maria Chiara Angelini, Carlo Lucibello, Giorgio Parisi, Gianmarco Perrupato, Federico Ricci-Tersenghi, and Tommaso Rizzo, "Unexpected Upper Critical Dimension for Spin Glass Models in a Field Predicted by the Loop Expansion around the Bethe Solution at Zero Temperature," in Physical Review Letters, 128, 075702. DOI: https://doi.org/10.1103/PhysRevLett.128.075702.