Il cielo della matematica e' pieno di stelle

Erio Castagnoli

Ci sono persone che riescono a trovare la bellezza nel formalismo rigoroso ed elegante della matematica, proprio come altre la trovano nella natura o nell'arte (qualcuno potrebbe addirittura sostenere che la matematica sia arte, o natura, o entrambe). Il compianto professor Erio Castagnoli era senza dubbio un grande appassionato della matematica, e ha saputo trasmettere il suo amore e la sua passione per la matematica a diverse generazioni di studenti della Bocconi. Tra questi, molti sono diventati scienziati di spicco e docenti nelle migliori università di tutto il mondo. L'attività scientifica del professor Castagnoli ha toccato molte applicazioni rilevanti, spaziando dalle scienze delle decisioni alla finanza matematica. Tuttavia, il tratto comune che ha caratterizzato il suo approccio è il gusto per l'astrazione matematica, ossia l'arte di individuare uno schema unificante in grado di spiegare una molteplicità di fenomeni.

Anche se Castagnoli ci ha lasciato nel 2019, le sue idee continuano a vivere e a produrre importanti sviluppi scientifici. Un recente articolo basato su un'intuizione che ha avuto negli ultimi giorni della sua vita – e di cui sono coautori Giacomo Cattelan (New York University), Fabio Maccheroni (Bocconi), Claudio Tebaldi (Bocconi) e Ruodu Wang (University of Waterloo, Canada) – indaga le misure stellate e ne illustra l'applicazione alla finanza e alla teoria delle decisioni.

Per avere un'idea di cosa sia una misura stellata, si consideri un mercato illiquido: se si vuole raddoppiare la quantità acquistata di un bene, ci si deve aspettare di pagare più del doppio del prezzo iniziale. Infatti, all'aumentare della quantità acquistata, il bene considerato diventa più scarso e di conseguenza anche il suo prezzo unitario aumenta. La traduzione in linguaggio matematico di questo fenomeno è che la relazione prezzo-quantità è convessa. Tuttavia, un meccanismo economico di questo tipo non richiede necessariamente che la convessità sia soddisfatta ovunque: se la funzione prezzo-quantità è normalizzata, cioè posta a zero in zero, allora la convessità è richiesta solo in zero. Le funzioni che soddisfano quest'ultima proprietà sono dette stellate all'origine. È interessante notare che tutte le funzioni convesse normalizzate sono stellate all'origine, mentre il viceversa non è generalmente valido.



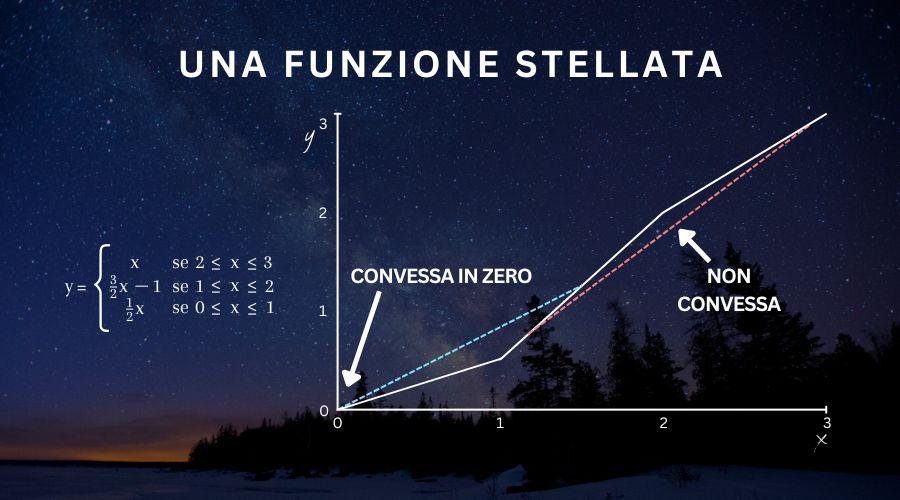
Ci si potrebbe chiedere se le funzioni stellate ma non convesse siano rilevanti ai fini delle applicazioni. Un buon punto di partenza per capirne la rilevanza è il fatto che qualsiasi misura realistica di rischio è stellata In particolare, per evitare che la mancanza di liquidità durante un'insolvenza propaghi la crisi al sistema finanziario, l'attuale regolamentazione impone alle stanze di compensazione e alle controparti centrali di depositare una certa quantità di denaro a garanzia (i cosiddetti requisiti di margine). Ebbene, si può dimostrare che tali requisiti devono essere il risultato di una funzione stellata, ma non necessariamente convessa, rispetto all'importo delle transazioni.

Inoltre, l'attrattiva delle misure di rischio stellate ha anche un fondamento nella teoria delle decisioni: esse modellizzano decisori istituzionali che, di fronte all'incertezza, adottino qualsiasi misura a loro disposizione per mitigarne gli effetti negativi e, all'aumentare del capitale totale dell'istituzione finanziaria, ne diminuiscano la parte esposta a tali effetti.

"Il messaggio principale dell'articolo," spiegano Tebaldi e Maccheroni, "è che meno è meglio: le misure stellate sono spesso sufficienti per modellare molti interessanti fenomeni non convessi che sono rilevanti per la pratica dell'economia. Quest'ultimo lavoro, di cui siamo coautori con il professor Castagnoli, mette in luce ancora una volta la sua importante eredità: la bellezza della matematica è la chiave per una conoscenza che faccia la differenza".

Erio Castagnoli, Giacomo Cattelan, Fabio Maccheroni, Claudio Tebaldi, Ruodu Wang (2022). "Star-Shaped Risk Measures." Operations Research 70(5): 2637-2654. https://doi.org/10.1287/opre.2022.2303.