Come sintetizzare grafi e ipergrafi

Le reti sono ovunque: che si tratti di persone, proteine o regioni cerebrali - solo per citare alcuni esempi - considerare gli individui senza le loro interazioni ci mostra un solo lato della medaglia, talvolta ancora meno. I dati di rete contengono queste preziose interazioni, ma spesso sono più che big data: sono dataset enormi. Basti pensare che i tre milioni di persone che vivono nell'area metropolitana di Milano possono stabilire milioni di milioni di possibili interazioni. Luca Trevisan, professore ordinario di informatica presso il Dipartimento di Scienze delle Decisioni della Bocconi, ha recentemente pubblicato un articolo sugli algoritmi che permettono di sintetizzare queste strutture di dati, rendendole così trattabili, preservando le informazioni in esse contenute.

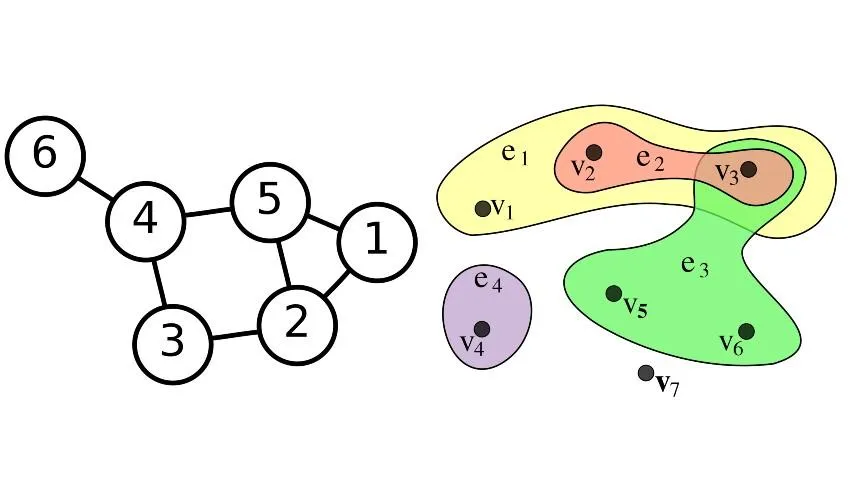
Da un punto di vista matematico, le reti possono essere rappresentate sotto forma di grafi, che consistono in un insieme di vertici (o nodi), che rappresentano gli individui, e un insieme di archi, ognuno dei quali unisce una coppia di nodi e rappresenta un'interazione tra gli individui corrispondenti. Gli ipergrafi generalizzano questa costruzione, permettendo a un arco di unire un numero qualsiasi di vertici, e possono essere usati per rappresentare modelli di connettività più complessi. La memoria necessaria per salvare un grafo e il tempo necessario per eseguire un algoritmo su di esso dipendono spesso dal numero di archi. Nel caso di un grafo con molti archi (un grafo denso) il numero di archi può essere dell'ordine del quadrato del numero dei vertici. Questo rende i grafi densi costosi da gestire, sia in termini di memoria che di tempo di calcolo.

Le tecniche di sparsificazione risolvono questo problema sostituendo il grafo originale con un grafo che abbia meno archi (sullo stesso insieme di nodi) ma che conservi alcune caratteristiche rilevanti del grafo originale. Una banale strategia di sparsificazione consiste nello scartare alcuni degli archi originali scegliendoli casualmente. Questo generalmente non funziona, perché - a seconda della proprietà del grafo da conservare - alcuni archi sono più importanti di altri. Per esempio, si consideri un grafo in cui i nodi sono chiaramente raggruppati in comunità e all'interno di ogni comunità i nodi sono molto densamente connessi, mentre pochissimi archi collegano nodi di comunità diverse. Se si vuole preservare il numero di archi da attraversare per passare da un vertice all'altro, allora gli archi che uniscono comunità diverse sono molto più importanti di quelli all'interno della stessa comunità. È quindi necessaria una strategia più elaborata di un campionamento casuale degli archi da scartare.

Per quanto riguarda i grafi, questo problema ha ricevuto molta attenzione nel corso degli anni e sono disponibili diversi algoritmi di sparsificazione. Purtroppo, i metodi esistenti per i grafi non possono essere semplicemente estesi agli ipergrafi.

"La ragione", spiega Trevisan, "è che la matematica che sta dietro ai grafi (matrici e algebra lineare) è diversa da quella che sta dietro agli ipergrafi, che coinvolge oggetti matematici più complessi chiamati tensori. Per questo motivo, dobbiamo progettare nuove tecniche per i grafi che siano estensibili agli ipergrafi. In questo senso, vedo la sparsificazione come un terreno di prova per ripensare gli algoritmi per i grafi".

Questo approccio è valso a Trevisan un prestigioso Advanced ERC Grant quinquennale, iniziato nel 2019. "Il primo anno di progetto ha già prodotto risultati entusiasmanti", dice Trevisan, "e siamo fiduciosi che il futuro produrrà ulteriori progressi. Si tratta di un'area di ricerca davvero interessante, che si colloca al crocevia tra matematica e informatica e può così contribuire ad entrambe le discipline".

N. Bansal, O. Svensson e L. Trevisan, "New notions and constructions of sparsification for graphs and hypergraphs", in 2019 IEEE 60th Annual Symposium on Foundations of Computer Science (FOCS).

Immagini:
By User:AzaToth - Image:6n-graf.png simlar input data, Public Domain, https://commons.wikimedia.org/w/index.php?curid=820489
By Hypergraph.svg: Kilom691derivative work: Pgdx (talk) - Hypergraph.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10687664